javascript - 算法:給一個數字,求有多少種方法相加等于這個數?
問題描述
比如8,可以有 4加4,2加5加1等,共有多少種方式,并列出所有方式集合
問題解答
回答1:實數無解
負數無解
如果數字的個數一定很簡單,兩個的話枚舉一半即可,多個可以參考下面的算法,修改為固定長度即可
如果數字的個數不一定,則也不能存在 0;參考一下
按公式的長度來遍歷遞歸,因為可以剪枝,效率可觀
function count (num) { if (!(num > 1)) { return [] } var equations = [] var eq = [] for (let len = 2; len <= num; len += 1) { _countByLen(num, eq, 0, len, 0) } return equations function _countByLen (num, eq, i, len, sum) { if (i === len) { if (sum === num) {equations.push(eq.join(’+’)) } return } for (let n = eq[i - 1] || 1; n < num; n += 1) { let newSum = n + sum if (newSum > num) { break } eq[i] = n _countByLen(num, eq, i + 1, len, newSum) } }}count(5) // [’1+4’, ’2+3’, ’1+1+3’, ’1+2+2’, ’1+1+1+2’, ’1+1+1+1+1’]
一開始想到的方式,將 1~n 每個的公式結果緩存起來遞歸,存起來很浪費空間,反復遍歷也很慢
function count (num) { if (!(num > 1)) { return [] } var equations = [,[[1]]] _count(num) return equations[num].slice(0, -1).map(eq => eq.join(’+’)) function _count (num) { if (equations[num]) { return equations[num] } let halfNum = Math.floor(num / 2) let eqNum = [] // 即 equations[num] for (let n = 1; n <= halfNum; n += 1) { _count(num - n).forEach(eq => {if (n <= eq[0]) { eqNum.push([n].concat(eq))} }) } eqNum.push([num]) equations[num] = eqNum return eqNum }}count(5) // ['1+1+1+1+1', '1+1+1+2', '1+1+3', '1+2+2', '1+4', '2+3']回答2:
如果是實數.. 這題沒什么意義
寫個兩兩相加的
這里寫個遞歸把.. 我也只懂一點點遞歸。。
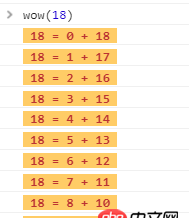
Rvar color = ’’; var wow = (n, i = 0) => { if (i > n / 2) return ; else {console.log(`%c ${n} = ${i} + ${n - i} `, color); wow(n, i + 1); }}S

無解只是你沒有給足條件,正整數是可以做的。用最簡單的遞歸,時間復雜度是接受不了的。用n=100程序直接就崩了我用的動態規劃,用一個矩陣保存s[i,j]保存對應的結果,這樣就不需要每次都重新算出之前的結果。其中si,j,i=n,以j開頭的組合數量,因為沒有0的情況,所以是s[i,0]我放的是s[i,1]+s[i,2]+...+s[i,j]的結果例如s[5,1],就是表示n=5,1+1+1+1+1,1+1+1+2,1+1+1+3,1+1+1+4,1+2+2,5種情況,其實按照這種方式可以很容易看出s[i,1]=s[i-1,0],故s[i,0]=s[i,1]+s[i,2]+...+s[i,j]s[i,0]=s[i-1,0]+s[i,2]+...+s[i,j]其中我們去掉重復的條件,就只需要計算到s[i,i],s[i,0]=s[i-1,0]+...+s[i,i]由于s[i,i]=1,所以最后只需要計算出s[i,2]+s[i,3]+...+s[i,i-1]的結果由于后來的數的組合方式都可以重之前的組合拼接出來,同s[i,1] = s[i-1,0],s[i,j] = s[i-j,k],其中j > 1, j <= k <= i下面是偽代碼
function(s, n) { s <= {0,0}; for(i = 1 to n)for (j = 1 to floor(i/2) ) if(j = 1) s[i][j] = s[i-1][0] else temp = 0;for(k = j to i) temp += s[i-j][k]s[i][j] = temp s[i][0] += s[i][j]s[i][j] = 1,s[i][0]++ return s}
下面是PHP實現的
function calculate(&$s, $n) { for( $i = 1; $i <= $n; $i++ ) {$s[$i][0] = 0;for( $j = 1; $j <= floor($i/2); $j++ ) { //以1開頭的,等于上一次計算結果 if( $j == 1 ) {$s[$i][$j] = $s[$i - 1][0]; } else {$temp = 0;for ($k = $j; $k <= $i; $k++) { if( isset($s[$i - $j][$k]) ) {$temp += $s[$i - $j][$k]; }}$s[$i][$j] = $temp; } $s[$i][0] += $s[$i][$j];}//對角線,加上自身$s[$i][$i] = 1;$s[$i][0]++; }}
感覺還可以再優化,計算si,j>1的情況可以預先保存之前組合的數量,通過空間換時間。希望對你有幫助
回答4:這個東西有一個函數叫 拆分函數P我之前做過一個跟這個有關的小算法題 神的90億名字不過我的題目中只需要求出整數拆分的數目,沒有涉及具體的組合,在上面那篇拆分函數P中估計有涉及到
回答5:這種算法邏輯最好有一定的限定條件,我姑且認為有指定數量的元數字和目標數字。
Java版本:
import java.util.ArrayList;import java.util.Arrays;class SumSet { static void sum_up_recursive(ArrayList<Integer> numbers, int target, ArrayList<Integer> partial) { int s = 0; for (int x: partial) s += x; if (s == target) System.out.println('sum('+Arrays.toString(partial.toArray())+')='+target); if (s >= target) return; for(int i=0;i<numbers.size();i++) { ArrayList<Integer> remaining = new ArrayList<Integer>(); int n = numbers.get(i); for (int j=i+1; j<numbers.size();j++) remaining.add(numbers.get(j)); ArrayList<Integer> partial_rec = new ArrayList<Integer>(partial); partial_rec.add(n); sum_up_recursive(remaining,target,partial_rec); } } static void sum_up(ArrayList<Integer> numbers, int target) {sum_up_recursive(numbers,target,new ArrayList<Integer>()); } public static void main(String args[]) {Integer[] numbers = {3,9,8,4,5,7,10};int target = 15;sum_up(new ArrayList<Integer>(Arrays.asList(numbers)),target); }}
C#版本:
public static void Main(string[] args){ List<int> numbers = new List<int>() { 3, 9, 8, 4, 5, 7, 10 }; int target = 15; sum_up(numbers, target);}private static void sum_up(List<int> numbers, int target){ sum_up_recursive(numbers, target, new List<int>());}private static void sum_up_recursive(List<int> numbers, int target, List<int> partial){ int s = 0; foreach (int x in partial) s += x; if (s == target)Console.WriteLine('sum(' + string.Join(',', partial.ToArray()) + ')=' + target); if (s >= target)return; for (int i = 0; i < numbers.Count; i++) {List<int> remaining = new List<int>();int n = numbers[i];for (int j = i + 1; j < numbers.Count; j++) remaining.Add(numbers[j]);List<int> partial_rec = new List<int>(partial);partial_rec.Add(n);sum_up_recursive(remaining, target, partial_rec); }}
Ruby版本:
def subset_sum(numbers, target, partial=[]) s = partial.inject 0, :+# check if the partial sum is equals to target puts 'sum(#{partial})=#{target}' if s == target return if s >= target (0..(numbers.length - 1)).each do |i| n = numbers[i] remaining = numbers.drop(i+1) subset_sum(remaining, target, partial + [n]) endendsubset_sum([3,9,8,4,5,7,10],15)
Python版本:
def subset_sum(numbers, target, partial=[]): s = sum(partial) # check if the partial sum is equals to target if s == target: print 'sum(%s)=%s' % (partial, target) if s >= target:return for i in range(len(numbers)):n = numbers[i]remaining = numbers[i+1:]subset_sum(remaining, target, partial + [n]) if __name__ == '__main__': subset_sum([3,9,8,4,5,7,10],15) #輸出: #sum([3, 8, 4])=15 #sum([3, 5, 7])=15 #sum([8, 7])=15 #sum([5, 10])=15
如果給定條件是正數的話,把數組換成1~N。這個邏輯同樣適用負數。
回答6:這個算法還是比較簡單的如果要分解的數為雙數 比如 18 那么幾乎它的結果會是(18/2+1)種組合 然后第一個數從0開始遞增,第二個數從最大值遞減即可如果為單數 17,那么可以讓它加1后再除以2,又變成(18/2)了,然后第一個數從0開始遞增,第二個數從最大值遞減即可

 網公網安備
網公網安備