import numpy as np #矩陣運算import matplotlib.pyplot as plt #可視化import random #產(chǎn)生數(shù)據(jù)擾動2. 產(chǎn)生數(shù)據(jù)

擬合曲線 y = 2 × x2 + x + 1

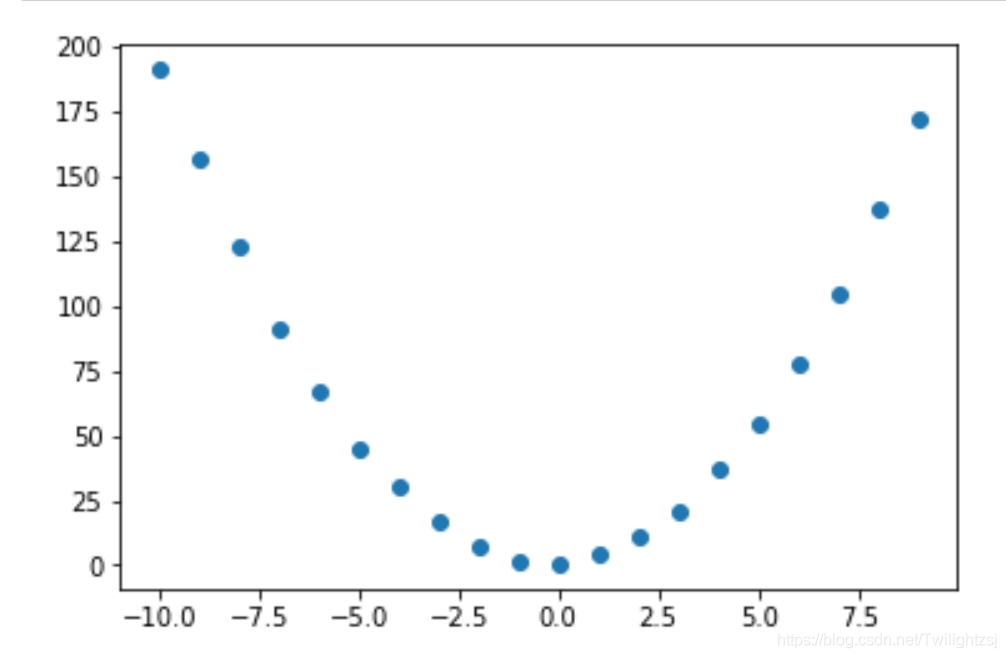
X_m = np.mat([[i**2, i, 1] for i in range(-10,10)]) #矩陣類型，用于運算y_m = np.mat([[2*x[0,0]+x[0,1]+1+random.normalvariate(0,1)] for x in X_m]) #矩陣類型，用于運算X_a = np.asarray(X_m[:,1].T)[0] #array類型，用于可視化y_a = np.asarray(y_m.T)[0] #array類型，用于可視化plt.scatter(X_a, y_a) #顯示數(shù)據(jù)plt.show()

def BGD(X,y,w0,step,e): #批量梯度下降法 n=0 while n<=10000: w1 = w0-step*X.T.dot(X.dot(w0)-y)/X.shape[0] dw = w1-w0; if dw.dot(dw.T)[0,0] <= e**2: return w1 n += 1 w0 = w1 return w14. 計算

w_m = BGD(X_m,y_m,np.mat([[5],[3],[2]]),1e-4,1e-20) #可自行調(diào)參w_a = np.asarray(w_m.T)[0]print(w_a)

array([1.99458492, 0.91587829, 1.48498921])

5. 評價( R 2)

y_mean = y_a.mean()y_pre = np.array([w_a[0]*x[0,0]+w_a[1]*x[0,1]+w_a[2] for x in X_m])SSR = ((y_pre-y_mean)**2).sum()SST = ((y_a-y_mean)**2).sum()R2 = SSR/SSTprint(R2)

0.9845542903194531我們可以認為擬合效果不錯。如果 R 2 R^{2} R2的值接近0，可能需要重新調(diào)參。

X = np.linspace(-10,10,50)y = np.array([w_a[0]*x**2+w_a[1]*x+w_a[2] for x in X])plt.scatter(X_a,y_a)plt.plot(X,y)plt.show()

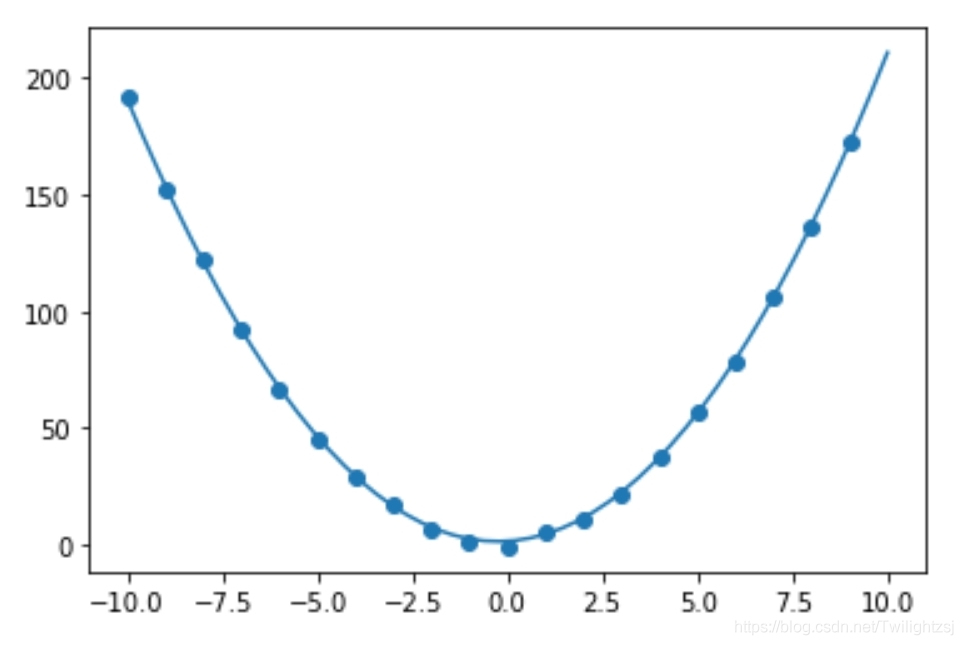
到此這篇關(guān)于Python實現(xiàn)批量梯度下降法(BGD)擬合曲線的文章就介紹到這了,更多相關(guān)Python 批量梯度下降內(nèi)容請搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！