這里分享一些軌跡聚類的基本方法，涉及軌跡距離的定義、kmeans聚類應(yīng)用。需要使用的python庫如下

import pandas as pdimport numpy as npimport randomimport osimport matplotlib.pyplot as pltimport seaborn as snsfrom scipy.spatial.distance import cdistfrom itertools import combinationsfrom joblib import Parallel, delayedfrom tqdm import tqdm數(shù)據(jù)讀取

假設(shè)數(shù)據(jù)是每一條軌跡一個(gè)excel文件，包括經(jīng)緯度、速度、方向的航班數(shù)據(jù)。我們從文件中讀取該數(shù)據(jù)，保存在字典中。獲取數(shù)據(jù)的地址，假設(shè)在多個(gè)文件中

def get_alldata_path(path): all_path = pd.DataFrame(columns=[’path_root’,’path0’,’path1’,’path2’,’path’,’datalist’]) path0 = os.listdir(path) for path_temp0 in path0: path1 = os.listdir(path+path_temp0) for path_temp1 in path1: path2 = os.listdir(path+path_temp0+’’+path_temp1) for path_temp2 in path2:path3 = os.listdir(path+path_temp0+’’+path_temp1+’’+path_temp2)all_path.loc[all_path.shape[0]] = [path,path_temp0,path_temp1,path_temp2, path+path_temp0+’’+path_temp1+’’+path_temp2+’’, path3] return all_path

這樣你就可以得到你的數(shù)據(jù)的地址，方便后面讀取需要的數(shù)據(jù)

#設(shè)置數(shù)據(jù)根目錄path = ’yourpath’#獲取所有數(shù)據(jù)地址data_path = get_alldata_path(path)

讀取數(shù)據(jù)，保存成字典格式，字典的key是這條軌跡的名稱，value值是一個(gè)DataFrame，需要包含經(jīng)緯度信息。

def read_data(data_path,idxs): ’’’ 功能：讀取數(shù)據(jù) ’’’ data = {} for idx in idxs: path_idx = data_path[’path’][idx] for dataname in data_path[’datalist’][idx]: temp = pd.read_excel(path_idx+dataname,header=None) temp = temp.loc[:,[4,5,6,8]] temp.replace(’none’,np.nan,inplace=True) temp.replace(’Trak’,np.nan,inplace=True) temp = temp.dropna().astype(float) temp.columns = [’GPSLongitude’,’GPSLatitude’,’direction’,’speed’] data[str(idx)+’_’+dataname] = temp return data

讀取你想要的數(shù)據(jù)，前面讀取到的地址也是一個(gè)DataFrame，選擇你想要進(jìn)行聚類的數(shù)據(jù)讀取進(jìn)來。

#讀取你想要的數(shù)據(jù)idxs = [0,1,2]data = read_data(data_path,idxs)定義不同軌跡間的距離

這里使用了雙向的Hausdorff距離（雙向豪斯多夫距離）給定兩條軌跡A和B,其中軌跡A上有n個(gè)點(diǎn),軌跡B上有m個(gè)點(diǎn)。它們之間的空間相似距離d定義為:

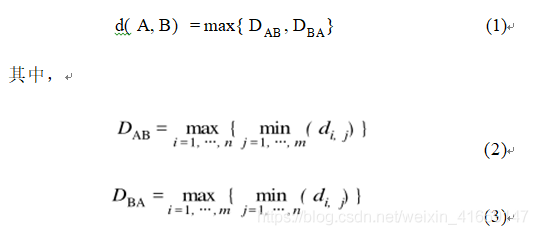
其中，di ,j 是一條軌跡上的第 i個(gè)點(diǎn)到另一條軌跡上的 第 j 個(gè) 點(diǎn)之間的多因素歐氏距離。可見, 如果軌跡 A 和 B 越相似, 它們之間的距離就越小, 反之則越大。

def OneWayHausdorffDistance(ptSetA, ptSetB): # 計(jì)算任意向量之間的距離，假設(shè)ptSetA有n個(gè)向量，ptSetB有m個(gè)向量 # 得到矩陣C（n行m列）Cij代表A中都第i個(gè)向量到B中第j向量都距離 dist = cdist(ptSetA, ptSetB, metric=’euclidean’) # np.min(dist,axis=1):計(jì)算每一行的的最小值 # 即：固定點(diǎn)集A的值，求點(diǎn)集A中到集合B的最小值 return np.max(np.min(dist, axis=1))# 計(jì)算雙向的Hausdorff距離=====>H(ptSetA,ptSetB)=max(h(ptSetA,ptSetB),h(ptSetB,ptSetA))# ptSetA：輸入的第一個(gè)點(diǎn)集# ptSetB：輸入的第二個(gè)點(diǎn)集# Hausdorff距離度量了兩個(gè)點(diǎn)集間的最大不匹配程度def HausdorffDistance(ptSetA, ptSetB): # 計(jì)算雙向的Hausdorff距離距離 res = np.array([ OneWayHausdorffDistance(ptSetA, ptSetB), OneWayHausdorffDistance(ptSetB, ptSetA) ]) return np.max(res) 計(jì)算距離矩陣

每個(gè)軌跡數(shù)據(jù)都包含經(jīng)緯度、速度、方向，分別計(jì)算距離，然后根據(jù)一定的比例相加，活動(dòng)最終的距離。

def DistanceMat(data,w=[0.7,0.2,0.1]): ’’’ 功能：計(jì)算軌跡段的距離矩陣 輸出：距離矩陣 ’’’ #要計(jì)算的組合 ptCom = list(combinations(list(data.keys()),2)) #基于軌跡的距離 distance_tra = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)( data[ptSet1][[’GPSLongitude’,’GPSLatitude’]],data[ptSet2][[’GPSLongitude’,’GPSLatitude’]] ) for ptSet1,ptSet2 in ptCom) distancemat_tra = pd.DataFrame(ptCom) distancemat_tra[’distance’] = distance_tra distancemat_tra = distancemat_tra.pivot(index=0,columns=1,values=’distance’) for pt1 in data.keys(): distancemat_tra.loc[str(pt1),str(pt1)] = 0 distancemat_tra = distancemat_tra.fillna(0) distancemat_tra = distancemat_tra.loc[list(data.keys()),list(data.keys())] distancemat_tra = distancemat_tra+distancemat_tra.T #基于方向的距離 distance_speed = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)( data[ptSet1][[’speed’]],data[ptSet2][[’speed’]] ) for ptSet1,ptSet2 in ptCom) distancemat_speed = pd.DataFrame(ptCom) distancemat_speed[’distance’] = distance_speed distancemat_speed = distancemat_speed.pivot(index=0,columns=1,values=’distance’) for pt1 in data.keys(): distancemat_speed.loc[str(pt1),str(pt1)] = 0 distancemat_speed = distancemat_speed.fillna(0) distancemat_speed = distancemat_speed.loc[list(data.keys()),list(data.keys())] distancemat_speed = distancemat_speed+distancemat_speed.T #基于方向的距離 distance_direction = Parallel(n_jobs=8,verbose=False)(delayed(HausdorffDistance)( data[ptSet1][[’direction’]],data[ptSet2][[’direction’]] ) for ptSet1,ptSet2 in ptCom) distancemat_direction = pd.DataFrame(ptCom) distancemat_direction[’distance’] = distance_direction distancemat_direction = distancemat_direction.pivot(index=0,columns=1,values=’distance’) for pt1 in data.keys(): distancemat_direction.loc[str(pt1),str(pt1)] = 0 distancemat_direction = distancemat_direction.fillna(0) distancemat_direction = distancemat_direction.loc[list(data.keys()),list(data.keys())] distancemat_direction = distancemat_direction+distancemat_direction.T distancemat_tra = (distancemat_tra-distancemat_tra.min().min())/(distancemat_tra.max().max()-distancemat_tra.min().min()) distancemat_speed = (distancemat_speed-distancemat_speed.min().min())/(distancemat_speed.max().max()-distancemat_speed.min().min()) distancemat_direction = (distancemat_direction-distancemat_direction.min().min())/(distancemat_direction.max().max()-distancemat_direction.min().min()) distancemat = w[0]*distancemat_tra+w[1]*distancemat_speed+w[2]*distancemat_direction return distancemat

使用前面讀取的數(shù)據(jù)，計(jì)算不同軌跡間的距離矩陣，缺點(diǎn)在于計(jì)算時(shí)間會隨著軌跡數(shù)的增大而指數(shù)增長。

distancemat = DistanceMat(data,w=[0.7,0.2,0.1])k-means聚類

獲得了不同軌跡間的距離矩陣后，就可以進(jìn)行聚類了。這里選擇k-means，為了得到更好的結(jié)果，聚類前的聚類中心選取也經(jīng)過了一些設(shè)計(jì)，排除了隨機(jī)選擇，而是選擇盡可能遠(yuǎn)的軌跡點(diǎn)作為 初始中心。初始化聚類“中心”。隨機(jī)選取一條軌跡作為第一類的中心, 即選取一個(gè)軌跡序列作為聚類的初始“中心。然后在剩下的 L - 1 個(gè)序列中選取一個(gè)序列 X 2 作為第二類的中心 C 2 , 設(shè)定一個(gè)閾值 q, 使其到第一類的中心 C 1 的距離大于q。

class KMeans: def __init__(self,n_clusters=5,Q=74018,max_iter=150): self.n_clusters = n_clusters #聚類數(shù) self.Q = Q self.max_iter = max_iter # 最大迭代數(shù) def fit(self,distancemat): #選擇初始中心 best_c = random.sample(distancemat.columns.tolist(),1) for i in range(self.n_clusters-1): best_c += random.sample(distancemat.loc[(distancemat[best_c[-1]]>self.Q)&(~distancemat.index.isin(best_c))].index.tolist(),1) center_init = distancemat[best_c] #選擇最小的樣本組合為初始質(zhì)心 self._init_center = center_init #迭代停止條件 iter_ = 0 run = True #開始迭代 while (iter_<self.max_iter)&(run==True): #聚類聚類標(biāo)簽更新 labels_ = np.argmin(center_init.values,axis=1) #聚類中心更新 best_c_ = [distancemat.iloc[labels_== i,labels_==i].sum().idxmin() for i in range(self.n_clusters)] center_init_ = distancemat[best_c_] #停止條件 iter_ += 1 if best_c_ == best_c: run = False center_init = center_init_.copy() best_c = best_c_.copy() #記錄數(shù)據(jù) self.labels_ = np.argmin(center_init.values,axis=1) self.center_tra = center_init.columns.values self.num_iter = iter_ self.sse = sum([sum(center_init.iloc[self.labels_==i,i]) for i in range(self.n_clusters)])

應(yīng)用聚類，根據(jù)平方誤差和SSE結(jié)合手肘法確定最佳的聚類數(shù)，使用最佳的聚類數(shù)獲得最后聚類模型。

#聚類，保存不同的sseSSE = []for i in range(2,30): kmeans = KMeans(n_clusters=i,Q=0.01,max_iter=150) kmeans.fit(distancemat) SSE.append(kmeans.sse)#畫圖plt.figure(0)plt.plot(SSE)plt.show()#使用最好的結(jié)果進(jìn)行聚類n_clusters=12kmeans = KMeans(n_clusters=n_clusters,Q=0.01,max_iter=150)kmeans.fit(distancemat)kmeans.sse #輸出ssekmeans.labels_ #輸出標(biāo)簽kmeans.center_tra #輸出聚類中心#畫圖，不同類的軌跡使用不同的顏色plt.figure(1)for i in range(n_clusters): for name in distancemat.columns[kmeans.labels_==i]: plt.plot(data[name].loc[:,’GPSLongitude’],data[name].loc[:,’GPSLatitude’],c=sns.xkcd_rgb[list(sns.xkcd_rgb.keys())[i]])plt.show()#保存每一個(gè)軌跡屬于哪一類kmeans_result = pd.DataFrame(columns=[’label’,’id’])for i in range(n_clusters): kmeans_result.loc[i] = [i,distancemat.columns[kmeans.labels_==i].tolist()]

到此這篇關(guān)于python 基于空間相似度的K-means軌跡聚類的實(shí)現(xiàn)的文章就介紹到這了,更多相關(guān)python K-means軌跡聚類內(nèi)容請搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！