對(duì)一個(gè)有向無(wú)環(huán)圖(Directed Acyclic Graph簡(jiǎn)稱(chēng)DAG)G進(jìn)行拓?fù)渑判颍菍中所有頂點(diǎn)排成一個(gè)線性序列，使得圖中任意一對(duì)頂點(diǎn)u和v，若邊(u,v)∈E(G)，則u在線性序列中出現(xiàn)在v之前。

通常，這樣的線性序列稱(chēng)為滿足拓?fù)浯涡?Topological Order)的序列，簡(jiǎn)稱(chēng)拓?fù)湫蛄小：?jiǎn)單的說(shuō)，由某個(gè)集合上的一個(gè)偏序得到該集合上的一個(gè)全序，這個(gè)操作稱(chēng)之為拓?fù)渑判颉?/p>

在圖論中，由一個(gè)有向無(wú)環(huán)圖的頂點(diǎn)組成的序列，當(dāng)且僅當(dāng)滿足下列條件時(shí)，稱(chēng)為該圖的一個(gè)拓?fù)渑判颍ㄓ⒄Z(yǔ)：Topological sorting）：

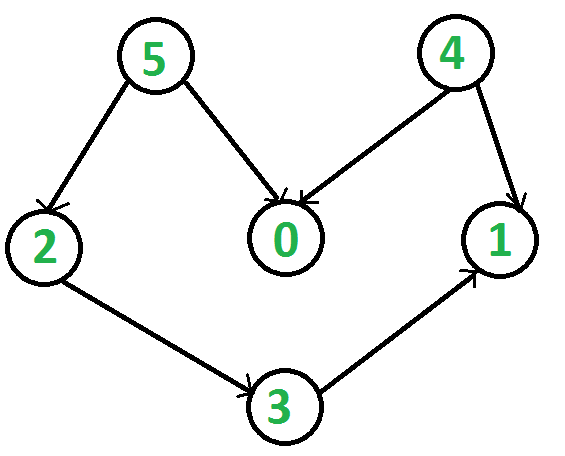
實(shí)例代碼

from collections import defaultdict class Graph: def __init__(self,vertices): self.graph = defaultdict(list) self.V = vertices def addEdge(self,u,v): self.graph[u].append(v) def topologicalSortUtil(self,v,visited,stack): visited[v] = True for i in self.graph[v]: if visited[i] == False: self.topologicalSortUtil(i,visited,stack) stack.insert(0,v) def topologicalSort(self): visited = [False]*self.V stack =[] for i in range(self.V): if visited[i] == False: self.topologicalSortUtil(i,visited,stack) print (stack) g= Graph(6) g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); print ('拓?fù)渑判蚪Y(jié)果：')g.topologicalSort()

執(zhí)行以上代碼輸出結(jié)果為：

拓?fù)渑判蚪Y(jié)果：

[5, 4, 2, 3, 1, 0]

實(shí)例擴(kuò)展：

def toposort(graph): in_degrees = dict((u,0) for u in graph) #初始化所有頂點(diǎn)入度為0 vertex_num = len(in_degrees) for u in graph: for v in graph[u]: in_degrees[v] += 1 #計(jì)算每個(gè)頂點(diǎn)的入度 Q = [u for u in in_degrees if in_degrees[u] == 0] # 篩選入度為0的頂點(diǎn) Seq = [] while Q: u = Q.pop() #默認(rèn)從最后一個(gè)刪除 Seq.append(u) for v in graph[u]: in_degrees[v] -= 1 #移除其所有指向 if in_degrees[v] == 0: Q.append(v) #再次篩選入度為0的頂點(diǎn) if len(Seq) == vertex_num: #如果循環(huán)結(jié)束后存在非0入度的頂點(diǎn)說(shuō)明圖中有環(huán)，不存在拓?fù)渑判? return Seq else: print('there’s a circle.')G = { ’a’:’bce’, ’b’:’d’, ’c’:’d’, ’d’:’’, ’e’:’cd’}print(toposort(G))

輸出結(jié)果：

[’a’, ’e’, ’c’, ’b’, ’d’]

到此這篇關(guān)于Python關(guān)于拓?fù)渑判蛑R(shí)點(diǎn)講解的文章就介紹到這了,更多相關(guān)Python 拓?fù)渑判騼?nèi)容請(qǐng)搜索好吧啦網(wǎng)以前的文章或繼續(xù)瀏覽下面的相關(guān)文章希望大家以后多多支持好吧啦網(wǎng)！