Python計(jì)算信息熵實(shí)例
計(jì)算信息熵的公式:n是類別數(shù),p(xi)是第i類的概率
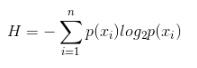
假設(shè)數(shù)據(jù)集有m行,即m個(gè)樣本,每一行最后一列為該樣本的標(biāo)簽,計(jì)算數(shù)據(jù)集信息熵的代碼如下:
from math import log def calcShannonEnt(dataSet): numEntries = len(dataSet) # 樣本數(shù) labelCounts = {} # 該數(shù)據(jù)集每個(gè)類別的頻數(shù) for featVec in dataSet: # 對(duì)每一行樣本 currentLabel = featVec[-1] # 該樣本的標(biāo)簽 if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 shannonEnt = 0.0 for key in labelCounts: prob = float(labelCounts[key])/numEntries # 計(jì)算p(xi) shannonEnt -= prob * log(prob, 2) # log base 2 return shannonEnt
補(bǔ)充知識(shí):python 實(shí)現(xiàn)信息熵、條件熵、信息增益、基尼系數(shù)
我就廢話不多說了,大家還是直接看代碼吧~
import pandas as pdimport numpy as npimport math## 計(jì)算信息熵def getEntropy(s): # 找到各個(gè)不同取值出現(xiàn)的次數(shù) if not isinstance(s, pd.core.series.Series): s = pd.Series(s) prt_ary = pd.groupby(s , by = s).count().values / float(len(s)) return -(np.log2(prt_ary) * prt_ary).sum()## 計(jì)算條件熵: 條件s1下s2的條件熵def getCondEntropy(s1 , s2): d = dict() for i in list(range(len(s1))): d[s1[i]] = d.get(s1[i] , []) + [s2[i]] return sum([getEntropy(d[k]) * len(d[k]) / float(len(s1)) for k in d])## 計(jì)算信息增益def getEntropyGain(s1, s2): return getEntropy(s2) - getCondEntropy(s1, s2)## 計(jì)算增益率def getEntropyGainRadio(s1, s2): return getEntropyGain(s1, s2) / getEntropy(s2)## 衡量離散值的相關(guān)性import mathdef getDiscreteCorr(s1, s2): return getEntropyGain(s1,s2) / math.sqrt(getEntropy(s1) * getEntropy(s2))# ######## 計(jì)算概率平方和def getProbSS(s): if not isinstance(s, pd.core.series.Series): s = pd.Series(s) prt_ary = pd.groupby(s, by = s).count().values / float(len(s)) return sum(prt_ary ** 2)######## 計(jì)算基尼系數(shù)def getGini(s1, s2): d = dict() for i in list(range(len(s1))): d[s1[i]] = d.get(s1[i] , []) + [s2[i]] return 1-sum([getProbSS(d[k]) * len(d[k]) / float(len(s1)) for k in d])## 對(duì)離散型變量計(jì)算相關(guān)系數(shù),并畫出熱力圖, 返回相關(guān)性矩陣def DiscreteCorr(C_data): ## 對(duì)離散型變量(C_data)進(jìn)行相關(guān)系數(shù)的計(jì)算 C_data_column_names = C_data.columns.tolist() ## 存儲(chǔ)C_data相關(guān)系數(shù)的矩陣 import numpy as np dp_corr_mat = np.zeros([len(C_data_column_names) , len(C_data_column_names)]) for i in range(len(C_data_column_names)): for j in range(len(C_data_column_names)): # 計(jì)算兩個(gè)屬性之間的相關(guān)系數(shù) temp_corr = getDiscreteCorr(C_data.iloc[:,i] , C_data.iloc[:,j]) dp_corr_mat[i][j] = temp_corr # 畫出相關(guān)系數(shù)圖 fig = plt.figure() fig.add_subplot(2,2,1) sns.heatmap(dp_corr_mat ,vmin= - 1, vmax= 1, cmap= sns.color_palette(’RdBu’ , n_colors= 128) , xticklabels= C_data_column_names , yticklabels= C_data_column_names) return pd.DataFrame(dp_corr_mat)if __name__ == '__main__': s1 = pd.Series([’X1’ , ’X1’ , ’X2’ , ’X2’ , ’X2’ , ’X2’]) s2 = pd.Series([’Y1’ , ’Y1’ , ’Y1’ , ’Y2’ , ’Y2’ , ’Y2’]) print(’CondEntropy:’,getCondEntropy(s1, s2)) print(’EntropyGain:’ , getEntropyGain(s1, s2)) print(’EntropyGainRadio’ , getEntropyGainRadio(s1 , s2)) print(’DiscreteCorr:’ , getDiscreteCorr(s1, s1)) print(’Gini’ , getGini(s1, s2))
以上這篇Python計(jì)算信息熵實(shí)例就是小編分享給大家的全部內(nèi)容了,希望能給大家一個(gè)參考,也希望大家多多支持好吧啦網(wǎng)。
相關(guān)文章:
1. Gitlab CI-CD自動(dòng)化部署SpringBoot項(xiàng)目的方法步驟2. Java封裝數(shù)組實(shí)現(xiàn)包含、搜索和刪除元素操作詳解3. Django:使用filter的pk進(jìn)行多值查詢操作4. JAVA上加密算法的實(shí)現(xiàn)用例5. 使用Python和百度語音識(shí)別生成視頻字幕的實(shí)現(xiàn)6. python基于socket模擬實(shí)現(xiàn)ssh遠(yuǎn)程執(zhí)行命令7. ASP刪除img標(biāo)簽的style屬性只保留src的正則函數(shù)8. idea打開多個(gè)窗口的操作方法9. ASP中解決“對(duì)象關(guān)閉時(shí),不允許操作。”的詭異問題……10. 淺談SpringMVC jsp前臺(tái)獲取參數(shù)的方式 EL表達(dá)式
 網(wǎng)公網(wǎng)安備
網(wǎng)公網(wǎng)安備