Java針對封裝數組的簡單復雜度分析方法
本文實例講述了Java針對封裝數組的簡單復雜度分析方法。分享給大家供大家參考,具體如下:
完成了數組的封裝之后我們還需對其進行復雜度分析:
此處的復雜度分析主要是指時間復雜度分析,算法的時間復雜度反映了程序執行時間隨輸入規模增長而增長的量級,在很大程度上能很好反映出算法的優劣與否。
1.簡單概念
在各種不同算法中,若算法中語句執行次數為一個常數,則時間復雜度為O(1),另外,在時間頻度不相同時,時間復雜度有可能相同,如T(n)=n2+3n+4與T(n)=4n2+2n+1它們的頻度不同,但時間復雜度相同,都為O(n2)。 按數量級遞增排列,常見的時間復雜度有:常數階O(1),對數階O(log2n),線性階O(n), 線性對數階O(nlog2n),平方階O(n2),立方階O(n3),..., k次方階O(nk),指數階O(2n)。隨著問題規模n的不斷增大,上述時間復雜度不斷增大,算法的執行效率越低。相關圖如下:
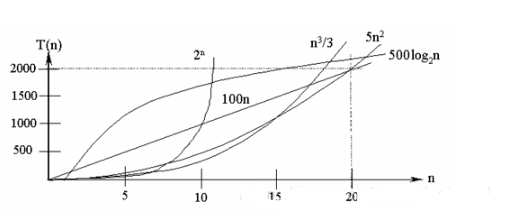
從圖中可見,我們應該盡可能選用多項式階O(nk)的算法,而不希望用指數階的算法。
見的算法時間復雜度由小到大依次為:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<Ο(n3)<…<Ο(2n)<Ο(n!)
2.大O簡單定義(非數學領域)
大O描述的是算法運行時間和輸入數據之間的關系
3.簡單程序時間復雜度分析

在上述中算法和n呈線性關系,那為什么要使用大O呢?稱作O(n)?
其實上述的程序中,實際的實際時間復雜度:T = c1*n + c2,在這里忽略了常數c1和c2。
因此:算法和N呈線性相關,取n的高階項,因為當n趨于無窮大的時候,低階項起的作用很小。
4.對動態數組的時間復雜度進行分析
(1)動態數組添加操作時間復雜度分析
(1)addLast(e)方法 :只需在最后位置添加 時間復雜度 為O(1)
(2)addFirst(e)方法,數組中均需向后移動一位 時間復雜度 為O(n)
(3)add(index,e)方法,在index位置插入e,時間復雜度與選擇的位置有關,選擇最后時間復雜度 為O(1);選擇第一個位置時間復雜度 為O(n);對于其他情況與概率有關,在平均情況下只需要移動n/2個位置 時間復雜度 為O(n/2)=O(n)
總的來說:數組添加的時間復雜度為O(n)(最壞情況考慮)
在添加的時候可能會觸發resize方法,需要移動n個元素到新數組中 時間復雜度 為O(n)

(2)動態數組刪除操作時間復雜度分析
相同的分析方法,可以得出刪除操作的時間復雜度

(3)動態數組修改操作時間復雜度分析
對于修改,只要通過索引找到即可進行修改,時間復雜度為O(1)

(4)動態數組查找操作時間復雜度分析


關于resize方法,我們完全使用最壞情況分析是不合理的,其分析情況我們將在下一節進行學習~
更多關于java相關內容感興趣的讀者可查看本站專題:《Java數組操作技巧總結》、《Java字符與字符串操作技巧總結》、《Java數學運算技巧總結》、《Java數據結構與算法教程》及《Java操作DOM節點技巧總結》
希望本文所述對大家java程序設計有所幫助。
相關文章:

 網公網安備
網公網安備