本文實(shí)例講述了Java刪除二叉搜索樹(shù)的任意元素的方法。分享給大家供大家參考，具體如下：

一.刪除思路分析

在刪除二叉搜索樹(shù)的任意元素時(shí)，會(huì)有三種情況：

1.1 刪除只有左孩子的節(jié)點(diǎn)

節(jié)點(diǎn)刪除之后，將左孩子所在的二叉樹(shù)取代其位置；連在原來(lái)節(jié)點(diǎn)父親元素右節(jié)點(diǎn)的位置，比如在圖中需要?jiǎng)h除58這個(gè)節(jié)點(diǎn)。

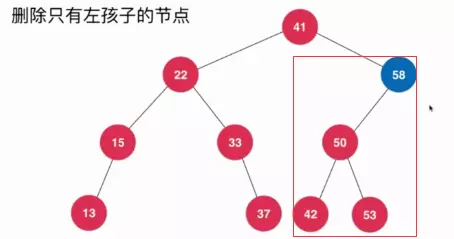
刪除58這個(gè)節(jié)點(diǎn)后，如下圖所示：

1.2 刪除只有右孩子的節(jié)點(diǎn)：

節(jié)點(diǎn)刪除之后，將右孩子所在的二叉樹(shù)取代其位置；連在原來(lái)節(jié)點(diǎn)的位置，比如在下圖中需要?jiǎng)h除58這個(gè)節(jié)點(diǎn)。

刪除58這個(gè)節(jié)點(diǎn)后，如下圖所示：

這里需要說(shuō)明說(shuō)一下，以上兩種情況其實(shí)包含了葉子節(jié)點(diǎn)情況的，我們可以把葉子節(jié)點(diǎn)理解成只有左孩子的節(jié)點(diǎn)，也可以把它理解為只有右孩子的節(jié)點(diǎn)，只不過(guò)左孩子、右孩子為null。

1.3 刪除包含左右孩子的節(jié)點(diǎn)

如下圖，二叉搜索樹(shù)包含有左右孩子，假設(shè)現(xiàn)需要?jiǎng)h除58這個(gè)節(jié)點(diǎn)。

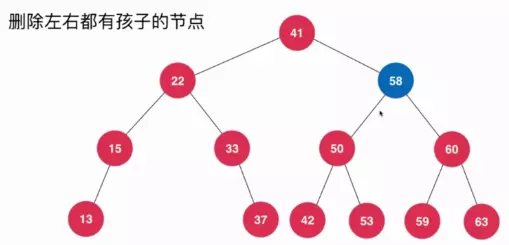
針對(duì)該種情況，分析如下：我們把58這個(gè)節(jié)點(diǎn)記為d節(jié)點(diǎn)（包含有左子樹(shù)與右子樹(shù)）,如下圖所示：

針對(duì)這種節(jié)點(diǎn)刪除情況需要把左子樹(shù)與右子樹(shù)融合起來(lái)，融合方法：從d這節(jié)點(diǎn)的左孩子與右孩子中找一個(gè)比d節(jié)點(diǎn)還要大的節(jié)點(diǎn)取代d節(jié)點(diǎn)，根據(jù)二叉搜索樹(shù)的性質(zhì)可知（左邊節(jié)點(diǎn)<當(dāng)前節(jié)點(diǎn)<右邊節(jié)點(diǎn)），這個(gè)需要被找的節(jié)點(diǎn)存在于d節(jié)點(diǎn)的右孩子節(jié)點(diǎn)中。

尋找規(guī)則：尋找需要被刪除節(jié)點(diǎn)58(d)的后繼的所有元素中，離 58 最近的且比 58 大的節(jié)點(diǎn)，在本例中為59這個(gè)節(jié)點(diǎn)【即右子樹(shù)中的最小值】，記為s，如下圖所示：

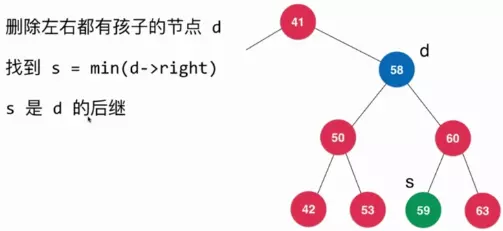
刪除步驟：

（1）從d的右子樹(shù)中刪除最小值，將刪除最小值s后的d的右子樹(shù), 變?yōu)閐后繼節(jié)點(diǎn)s的右孩子，如下圖所示：

（2）將d節(jié)點(diǎn)（58節(jié)點(diǎn)）的左子樹(shù)，變?yōu)楹罄^節(jié)點(diǎn)s(59節(jié)點(diǎn))的左子樹(shù)，如下圖所示：

(3)將后繼節(jié)點(diǎn)s（59節(jié)點(diǎn)）連接到d節(jié)點(diǎn)（58節(jié)點(diǎn)）父親節(jié)點(diǎn)的右邊，刪除d節(jié)點(diǎn)（58節(jié)點(diǎn)）后,后繼s節(jié)點(diǎn)（59節(jié)點(diǎn)）成為新的根，如下圖所示：

二、編碼實(shí)現(xiàn)二叉搜索樹(shù)的任意元素

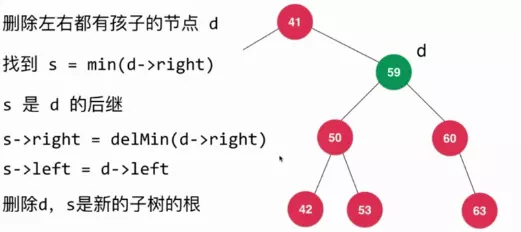
根據(jù)上述的分析，在此基礎(chǔ)上進(jìn)行編碼，刪除代碼如下：

//從二叉搜索樹(shù)中刪除元素為e的節(jié)點(diǎn) public void remove(E e) { root = remove(root, e); } //刪除以node為根的二叉搜索樹(shù)中值為e的節(jié)點(diǎn)，遞歸算法 //返回刪除節(jié)點(diǎn)后更新的二叉搜索樹(shù)的根 private Node remove(Node node, E e) { if (node == null) return null; if (e.compareTo(node.e) < 0) {//e<node.e (被刪除元素e小于當(dāng)前節(jié)點(diǎn)值e) node.left = remove(node.left, e); return node; } if (e.compareTo(node.e) > 0) {//e>node.e (被刪除元素e大于當(dāng)前節(jié)點(diǎn)值e) node.right = remove(node.right, e); return node; } else {//e==node.e (被刪除元素e等于當(dāng)前節(jié)點(diǎn)值e) //待刪除節(jié)點(diǎn)左子樹(shù)為空情況 if (node.left == null) {Node rightNode = node.right;node.right = null;size--;return rightNode; } //待刪除節(jié)點(diǎn)右子樹(shù)為空情況 if (node.right == null) {Node leftNode = node.left;node.left = null;size--;return leftNode; } //左右子樹(shù)均不為空 //方法：找到比待刪除節(jié)點(diǎn)大的最小節(jié)點(diǎn)，即待刪除節(jié)點(diǎn)右子樹(shù)的最小節(jié)點(diǎn) //用這個(gè)節(jié)點(diǎn)頂替待刪除節(jié)點(diǎn)的位置 Node successor = minimum(node.right); successor.right = removeMin(node.right); successor.left = node.left; node.left = node.right = null; return successor; } }

對(duì)于上述代碼中的minimum函數(shù)，在5.3節(jié)中已經(jīng)實(shí)現(xiàn)，此處同樣也把代碼列出來(lái)：

// 尋找二分搜索樹(shù)的最小元素 public E minimum() { if (size == 0) { throw new IllegalArgumentException('BST is empty'); } Node ninNode = minimum(root); return ninNode.e; } // 返回以node為根的二分搜索樹(shù)的最小值所在的節(jié)點(diǎn) private Node minimum(Node node) { if (node.left == null) { return node; } //返回相應(yīng)的節(jié)點(diǎn)的左子樹(shù)的最小值 return minimum(node.left); }

源碼地址 https://github.com/FelixBin/dataStructure/blob/master/src/BST/BST.java

更多關(guān)于java算法相關(guān)內(nèi)容感興趣的讀者可查看本站專題：《Java數(shù)據(jù)結(jié)構(gòu)與算法教程》、《Java操作DOM節(jié)點(diǎn)技巧總結(jié)》、《Java文件與目錄操作技巧匯總》和《Java緩存操作技巧匯總》

希望本文所述對(duì)大家java程序設(shè)計(jì)有所幫助。