python 解決微分方程的操作(數值解法)
對于一些微分方程來說,數值解法對于求解具有很好的幫助,因為難以求得其原方程。
比如方程:
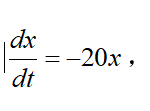
但是我們知道了它的初始條件,這對于我們疊代求解很有幫助,也是必須的。
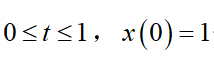
那么現在我們也用Python去解決這一些問題,一般的數值解法有歐拉法、隱式梯形法等,我們也來看看這些算法對疊代的精度有什么區別?
```python```pythonimport numpy as npfrom scipy.integrate import odeintfrom matplotlib import pyplot as pltimport os#先從odeint函數直接求解微分方程#創建歐拉法的類class Euler: #構造方法,當創建對象的時候,自動執行的函數 def __init__(self,h,y0):#將對象與對象的屬性綁在一起self.h = hself.y0 = y0self.y = y0self.n = 1/self.hself.x = 0self.list = [1]#歐拉法用list列表,其x用y疊加儲存self.list2 = [1]self.y1 = y0#改進歐拉法用list2列表,其x用y1疊加儲存self.list3 = [1]self.y2 = y0#隱式梯形法用list3列表,其x用y2疊加儲存 #歐拉法的算法,算法返回t,x def countall(self):for i in range(int(self.n)): y_dere = -20*self.list[i] #歐拉法疊加量y_dere = -20 * x y_dere2 = -20*self.list2[i] + 0.5*400*self.h*self.list2[i] #改進歐拉法疊加量 y_dere2 = -20*x(k) + 0.5*400*delta_t*x(k) y_dere3 = (1-10*self.h)*self.list3[i]/(1+10*self.h) #隱式梯形法計算 y_dere3 = (1-10*delta_t)*x(k)/(1+10*delta_t) self.y += self.h*y_dere self.y1 += self.h*y_dere2 self.y2 =y_dere3 self.list.append(float('%.10f' %self.y)) self.list2.append(float('%.10f'%self.y1)) self.list3.append(float('%.10f'%self.y2))return np.linspace(0,1,int(self.n+1)), self.list,self.list2,self.list3step = input('請輸入你需要求解的步長:')step = float(step)work1 = Euler(step,1)ax1,ay1,ay2,ay3 = work1.countall()#畫圖工具pltplt.figure(1)plt.subplot(1,3,1)plt.plot(ax1,ay1,’s-.’,MarkerFaceColor = ’g’)plt.xlabel(’橫坐標t’,fontproperties = ’simHei’,fontsize =20)plt.ylabel(’縱坐標x’,fontproperties = ’simHei’,fontsize =20)plt.title(’歐拉法求解微分線性方程步長為’+str(step),fontproperties = ’simHei’,fontsize =20)plt.subplot(1,3,2)plt.plot(ax1,ay2,’s-.’,MarkerFaceColor = ’r’)plt.xlabel(’橫坐標t’,fontproperties = ’simHei’,fontsize =20)plt.ylabel(’縱坐標x’,fontproperties = ’simHei’,fontsize =20)plt.title(’改進歐拉法求解微分線性方程步長為’+str(step),fontproperties = ’simHei’,fontsize =20)plt.subplot(1,3,3)plt.plot(ax1,ay3,’s-.’,MarkerFaceColor = ’b’)plt.xlabel(’橫坐標t’,fontproperties = ’simHei’,fontsize =20)plt.ylabel(’縱坐標x’,fontproperties = ’simHei’,fontsize =20)plt.title(’隱式梯形法求解微分線性方程步長為’+str(step),fontproperties = ’simHei’,fontsize =20)plt.figure(2)plt.plot(ax1,ay1,ax1,ay2,ax1,ay3,’s-.’,MarkerSize = 3)plt.xlabel(’橫坐標t’,fontproperties = ’simHei’,fontsize =20)plt.ylabel(’縱坐標x’,fontproperties = ’simHei’,fontsize =20)plt.title(’三合一圖像步長為’+str(step),fontproperties = ’simHei’,fontsize =20)ax = plt.gca()ax.legend((’$Eular$’,’$fixed Eular$’,’$trapezoid$’),loc = ’lower right’,title = ’legend’)plt.show()os.system('pause')
對于歐拉法,它的疊代方法是:
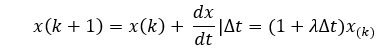
改進歐拉法的疊代方法:
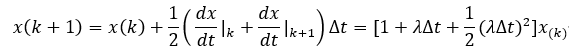
隱式梯形法:
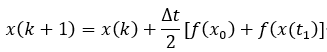
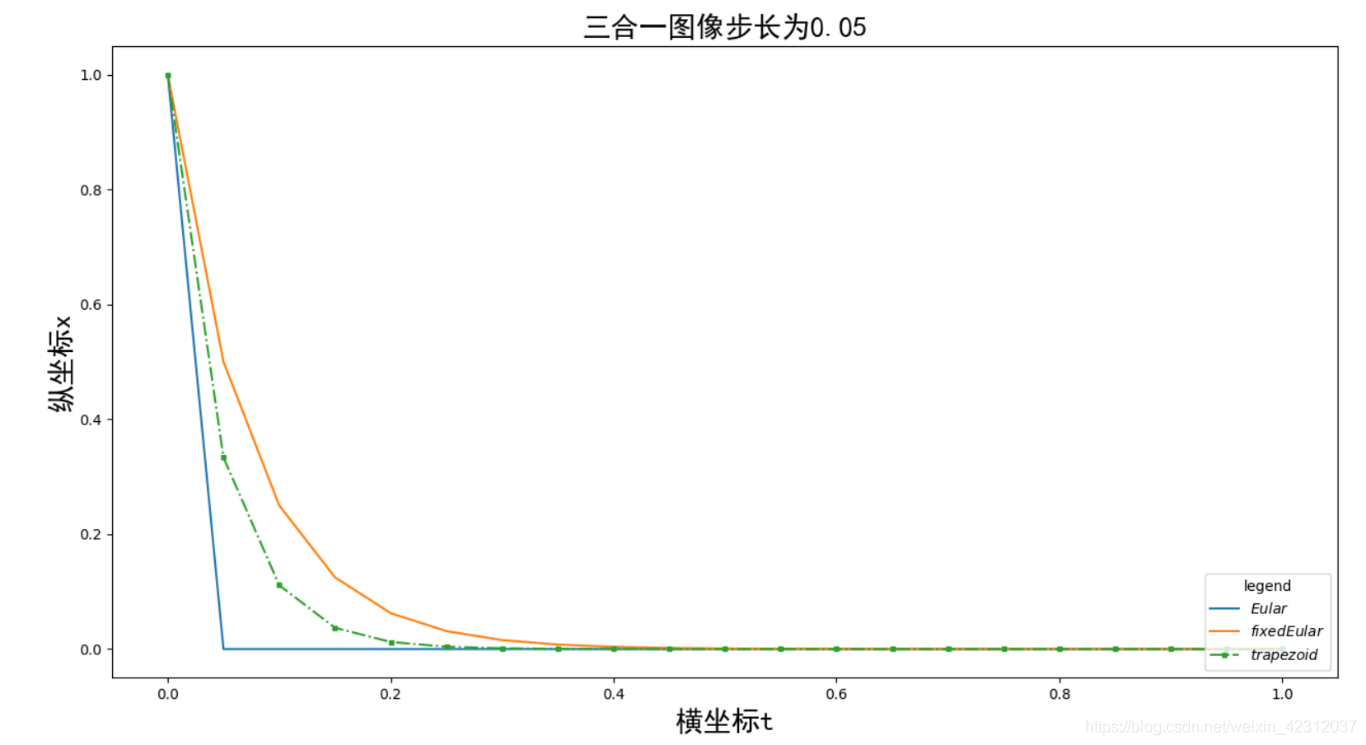
對于不同的步長,其求解的精度也會有很大的不同,我先放一幾張結果圖:
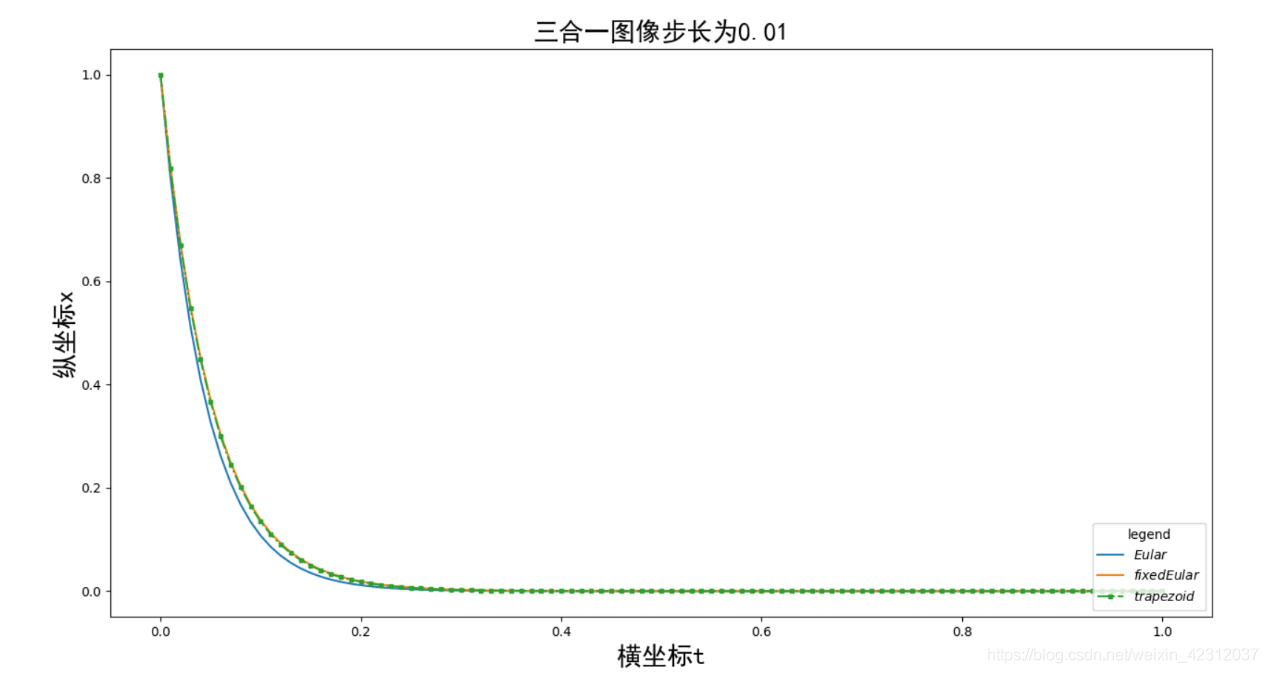
補充:基于python的微分方程數值解法求解電路模型
安裝環境包安裝numpy(用于調節range) 和 matplotlib(用于繪圖)
在命令行輸入
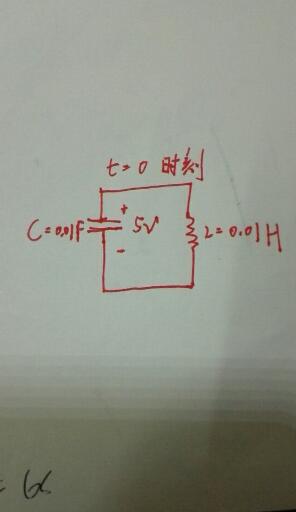
pip install numpy pip install matplotlib電路模型和微分方程模型1
無損害,電容電壓為5V,電容為0.01F,電感為0.01H的并聯諧振電路
電路模型1
微分方程1

微分方程2
相關文章:

 網公網安備
網公網安備